Equilibre stable et instable
3 participants
Page 1 sur 1
 Equilibre stable et instable
Equilibre stable et instable
Bonjour à tous: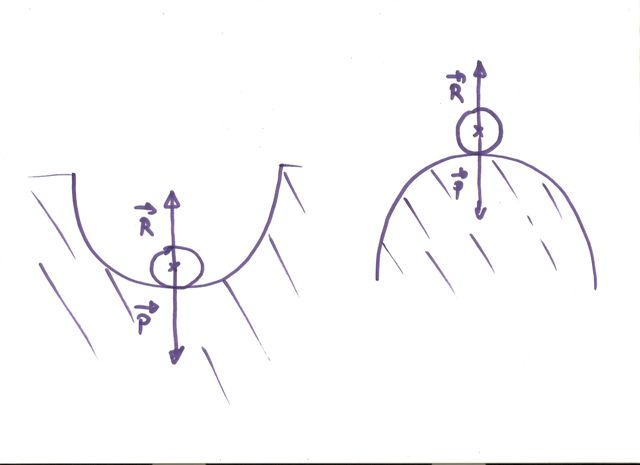
Voici un petit schéma où l'on voit deux positions d'équilibre d'une bille sans frottements.
Bien sur je suppose que tout est idéal,pas de frottements,référentiel terrestre,aucunes autres forces venant déranger tout ça etc...
Une question me tracasse:
pourquoi le schéma de gauche est-il un équilibre " stable " et celui de gauche "instable " ?
Je sais que si l'on fait quelques calculs pour un déplacement élémentaire pour chaque bille:
pour une on a a.v<0 et l'autre a.v>0 ce qui explique que l'une s'écarte de plus en plus de sa position d'équilibre.
Mais moi ce qui me dérange, d'après mes schémas, il n'y a aucune raison que l'une ou l'autre ne s'écarte plus facilement de sa position d'équilibre (bien sur sans qu'il y ait déplacement élémentaire)
J'espère avoir été des plus clair.

Voici un petit schéma où l'on voit deux positions d'équilibre d'une bille sans frottements.
Bien sur je suppose que tout est idéal,pas de frottements,référentiel terrestre,aucunes autres forces venant déranger tout ça etc...
Une question me tracasse:
pourquoi le schéma de gauche est-il un équilibre " stable " et celui de gauche "instable " ?
Je sais que si l'on fait quelques calculs pour un déplacement élémentaire pour chaque bille:
pour une on a a.v<0 et l'autre a.v>0 ce qui explique que l'une s'écarte de plus en plus de sa position d'équilibre.
Mais moi ce qui me dérange, d'après mes schémas, il n'y a aucune raison que l'une ou l'autre ne s'écarte plus facilement de sa position d'équilibre (bien sur sans qu'il y ait déplacement élémentaire)
J'espère avoir été des plus clair.
 Re: Equilibre stable et instable
Re: Equilibre stable et instable
Bonsoir,
La notion essentielle à considérer dans l'étude des stabilités d'équilibre, c'est l'énergie potentielle. Tu te rappelles peut être (sans doute...) que l'on peut exprimer la force qui provoque un mouvement en fonction de la variation d'énergie potentielle de la masse en mouvement (cas d'une force centrale bien sur!). Cela donne F = - dEp/dx, en supposant le mouvement unidimensionnel.
Si dEp/dx = 0, alors la force est nulle, et il n'y a pas de mouvement: c'est l'équilibre. Mais comment savoir si c'est un équilibre stable ou instable? En vérifiant si tu es sur un minimum de la courbe Ep(x) ou un maximum. Je ne ferais pas l'injure à un prof de math de lui dire comment faire! Et donc, si tu es sur un minimum (dans une cuvette - on dit "puit de potentiel"), ton équilibre est stable. Si tu es sur un maximum (au sommet de ta courbe) ton équilibre est instable.
La notion essentielle à considérer dans l'étude des stabilités d'équilibre, c'est l'énergie potentielle. Tu te rappelles peut être (sans doute...) que l'on peut exprimer la force qui provoque un mouvement en fonction de la variation d'énergie potentielle de la masse en mouvement (cas d'une force centrale bien sur!). Cela donne F = - dEp/dx, en supposant le mouvement unidimensionnel.
Si dEp/dx = 0, alors la force est nulle, et il n'y a pas de mouvement: c'est l'équilibre. Mais comment savoir si c'est un équilibre stable ou instable? En vérifiant si tu es sur un minimum de la courbe Ep(x) ou un maximum. Je ne ferais pas l'injure à un prof de math de lui dire comment faire! Et donc, si tu es sur un minimum (dans une cuvette - on dit "puit de potentiel"), ton équilibre est stable. Si tu es sur un maximum (au sommet de ta courbe) ton équilibre est instable.
 Re: Equilibre stable et instable
Re: Equilibre stable et instable
Oui si j'ai bien compris la courbe Ep(x) a la même forme que les cuvettes représentées.
 Re: Equilibre stable et instable
Re: Equilibre stable et instable
A peu près... En fait, tu peux la tracer en partant de l'équation de conservation de l'énergie totale du système E = 1/2*m(dx/dt)² + Ep(x) ou encore, en résolvant en dx/dt, dx/dt = (2/m * (E - Ep(x)))^1/2 . Cette petite équation t'explique pourquoi le mouvement du point massif n'est possible que si E > Ep à moins d'imaginer une vitesse imaginaire!fabien a écrit:Oui si j'ai bien compris la courbe Ep(x) a la même forme que les cuvettes représentées.
En passant, si tu sépares les variables x et t et que tu intègres, tu retrouves l'équation du mouvement rectiligne.
L'approche par l'énergie est la base de la mécanique lagrangienne et hamiltonienne, très usitée chez les quanticiens...
 Re: Equilibre stable et instable
Re: Equilibre stable et instable
On a Ep(x)=E-1/2*m(dx/dt)² mais si je trace cette courbe , elle est incurvée vers le bas ou si tu veux E''p(x)<0.En fait, tu peux la tracer en partant de l'équation de conservation de l'énergie totale du système E = 1/2*m(dx/dt)² + Ep(x)
Là je m'embrouille ou pas ?
 Re: Equilibre stable et instable
Re: Equilibre stable et instable
sans aborder le côté mathématique, on peut dire simplement que lorsque je déplace "à peine" la bille:
- elle part au loin pour un équilibre instable
- elle revient à sa position initial pour un équilibre stable
- elle part au loin pour un équilibre instable
- elle revient à sa position initial pour un équilibre stable

Babe- Nombre de messages : 26
Age : 36
Localisation : Grenoble
Date d'inscription : 23/11/2008
 Re: Equilibre stable et instable
Re: Equilibre stable et instable
Pour sur, mais je voulais à travers ma question savoir pourquoi si les deux positions étaient en position d'équilibre , pourquoi l'une était plus faible que l'autre.Babe a écrit:sans aborder le côté mathématique, on peut dire simplement que lorsque je déplace "à peine" la bille:
- elle part au loin pour un équilibre instable
- elle revient à sa position initial pour un équilibre stable
 Re: Equilibre stable et instable
Re: Equilibre stable et instable
La remarque de Babe n'est pas tout à fait anodine. La définition que les mécaniciens donnent de la stabilité (stable si d²E/dx² > 0 et instable si d²E/dx² <0) est assez théorique. Un système mécanique parfait pourrait rester dans un état métastable (d²E/dx² = 0) - en haut de la colline) éternellement si aucune perturbation élémentaire ne survenait jamais. Mais cette condition est inapplicable en physique : c'est strictement impossible.fabien a écrit:Pour sur, mais je voulais à travers ma question savoir pourquoi si les deux positions étaient en position d'équilibre , pourquoi l'une était plus faible que l'autre.Babe a écrit:sans aborder le côté mathématique, on peut dire simplement que lorsque je déplace "à peine" la bille:
- elle part au loin pour un équilibre instable
- elle revient à sa position initial pour un équilibre stable
Un système physique tend toujours à réduire son énergie totale, et donc dans notre exemple, son énergie mécanique. Lorsque la particule est en haut de la colline, il existe un seul moyen de réduire l'énergie du système : tomber. Lorsque la particule est dans le puit, il existe deux possibilités classiques: soit tu communiques à la particule suffisamment d'énergie pour sortir du puit et elle court vers un autre état stable, soit l'énergie communiquée n'est pas suffisante et elle reste dans son puit. Je te passe la possibilité quantique qui est l'effet tunnel.
 Re: Equilibre stable et instable
Re: Equilibre stable et instable
Ces explications me sont suffisantes, merci maintenant j'ai une autre vue sur le phénomène. 
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum